New Paper: Hunting for Primordial Black Holes, The O4 Sub-Solar Mass Bank
The Physics: Why Search Below \(1 M_\odot\)?
Standard stellar evolution tells us that black holes shouldn’t exist below roughly \(3 M_\odot\), and neutron stars likely have a minimum mass around \(1 M_\odot\). So, if we detect a compact object with mass \(m < 1 M_\odot\), it cannot be of stellar origin.
It would likely be a Primordial Black Hole (PBH), an object formed from the direct collapse of high-density fluctuations in the early universe, long before the first stars were born. Detecting a sub-solar mass (SSM) merger would not only be the first detection of a PBH but could also provide evidence that PBHs constitute a fraction of Dark Matter.
In the fourth observing run (O4) of LIGO-Virgo-KAGRA, we are searching for these elusive signals. But to find them, we needed a new template bank.
The Challenge: Geometric Breakdown
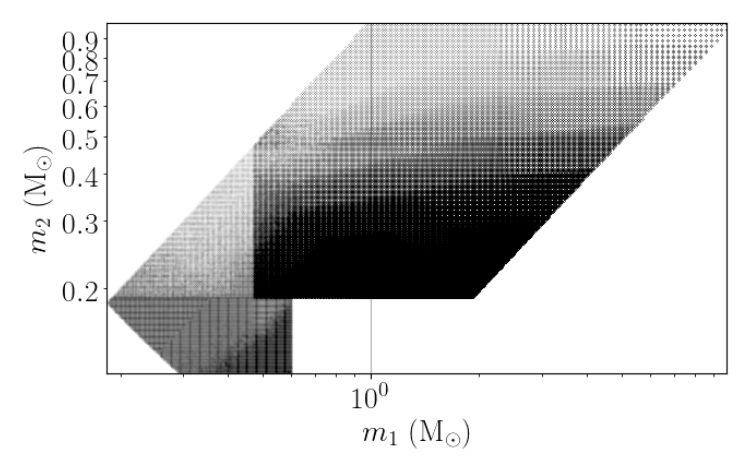
We used our geometric Treebank algorithm (described in my previous post) to generate this bank. However, pushing into the sub-solar mass regime (\(0.2 M_\odot - 1.0 M_\odot\)) broke the standard algorithm.
The signal manifold curvature scales with the number of wave cycles. For low-mass binaries, the signals are incredibly long (minutes long), making the metric \(g_{ij}\) vary rapidly. We encountered two major singularities: 1. Metric Instability: Numerical derivatives became unstable, leading to non-positive-definite metrics (negative eigenvalues). 2. Boundary Depletion: The “hard cut” at the boundary of the parameter space left the edges under-covered, leading to efficiency loss for the lowest mass signals.
The Solution: Neighborhood Estimation
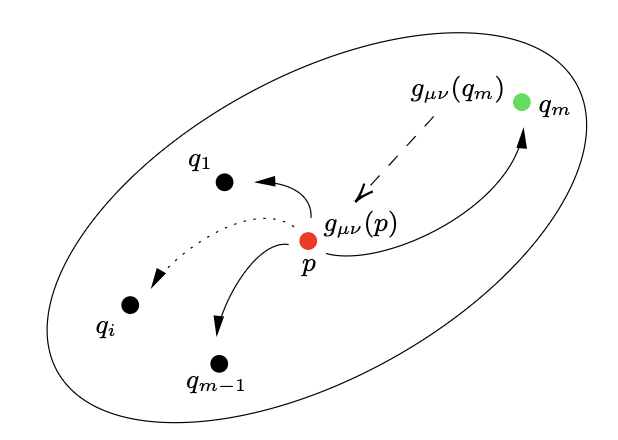
To solve the instability, we generalized the notion of the metric. Instead of calculating \(g_{ij}\) at a single point \(p\), we implemented Neighborhood Metric Estimation.
If the metric calculation fails at \(p\), we define a local “trust region” (a hyper-ellipsoid \(\mathcal{U}_p\)) and randomly sample points \(q_i \in \mathcal{U}_p\) until we find a stable metric. We then transport this metric back to \(p\). This allows the algorithm to “step over” numerical singularities while preserving the geometric structure.
We also implemented Boundary Padding, effectively generating a secondary “marginal” bank that specifically targets the edges of the parameter space, ensuring that signals right on the \(0.2 M_\odot\) line are recovered with full sensitivity.
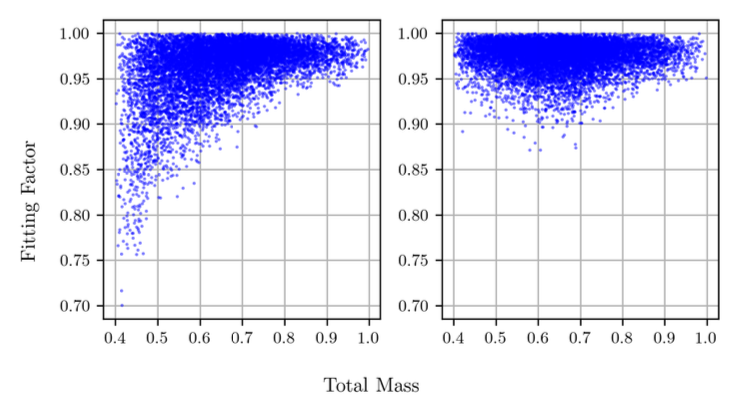
The Result: O4 SSM Bank
The final product is the O4 Sub-Solar Mass Template Bank detailed in our recent paper. [1]. It contains 3,452,006 templates covering component masses from \(0.2 M_\odot\) to \(10 M_\odot\).
This represents the first successful application of geometric manifold methods to this difficult corner of parameter space. It is currently being used in the GstLAL search pipeline to analyze O4 data. If there are Primordial Black Holes hiding in the noise, this is the net we built to catch them.